|
|
|
- Info
Barbara Frank
Research
Motion Planning in Environments with Deformable Objects
|
The ability to plan their own motions and to reliably execute them
is an important precondition for truly autonomous
robots. In our work, we consider the problem of motion planning for robots in environments
with non-rigid obstacles such as curtains or plants. We
combine probabilistic roadmap planning with a physical simulation of
object deformations to determine a path that optimizes the trade-off
between the deformation cost and the distance to be traveled. Our
approach utilizes Finite Element theory for computing the
deformation costs.
Carrying out the corresponding simulations during planning time,
however, is time-consuming. Therefore, we present
an approach to model object deformation cost functions based on
Gaussian process regression, which can be efficiently evaluated when
answering path queries. For stationary objects, the simulations
of robot motions to generate data for regression can be done in
a preprocessing step.
We implemented our approaches on real robots and applied the developed
planning framework to different platforms, a wheeled robot and a
manipulator with seven degrees of freedom. The examples below
demonstrate that our robots are able to successfully navigate in
environments with deformable obstacles.
|
|
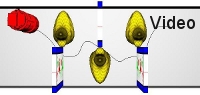
In this simulated planning example, the deformation of rubber ducks
is more expensive than the deformation of curtains. Accordingly, the
robot chooses a path that avoids the rubber ducks.
Query Time: 0.13s.
|
 |
This real world experiment demonstrates how our robot Albert
navigates in an environment with deformable curtains. Furthermore,
it shows how the robot performs a basic collision avoidance and is
able to distinguish allowed contacts with the curtains from
collisions with dynamic obstacles.
Query Time: 0.1s.
|
- Planning for Manipulators in 3D
|
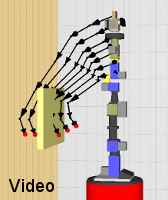
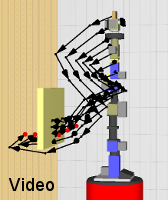
In this real-world planning example, the manipulator has to reach a
goal configuration behind a deformable foam mat. If deformable
obstacles are ignored, the shortest path to the goal is chosen (left
figure). The robot destroys the experimental setup when
executing
this path. Our planner, in contrast, chooses a path that trades off
deformation costs and motion costs (right figure). When
moving along this
trajectory, the robot keeps the deformation of the foam mat to a
minimum. The videos demonstrate how our manipulation robot Zora
executes the planned motions.
Query Time: 8.6s.
|


|
|
The robot has to move its endeffector to the target position behind the deformable teddy bear (indicated in red).
The left image shows the shortest path to the goal while the right image shows the computed path
that trades off path and deformation cost. The video
illustrates the execution of these paths in our deformation simulation.
|


|
|
The robot has to move its end effector from its current position to the target position
left of the deformable teddy bear (indicated in red). The left image shows the shortest
path to the goal while the right image shows the computed path that trades off path and deformation cost.
The video illustrates the execution
of these paths in our deformation simulation.
|
|
|









