The character type Char is an enumeration whose values represent Unicode characters [11]. The lexical syntax for characters is defined in Section 2.6; character literals are nullary constructors in the datatype Char. Type Char is an instance of the classes Read, Show, Eq, Ord, Enum, and Bounded. The toEnum and fromEnum functions, standard functions from class Enum, map characters to and from the Int type.
Note that ASCII control characters each have several representations in character literals: numeric escapes, ASCII mnemonic escapes, and the \^X notation. In addition, there are the following equivalences: \a and \BEL, \b and \BS, \f and \FF, \r and \CR, \t and \HT, \v and \VT, and \n and \LF.
A string is a list of characters:
type String = [Char]
Strings may be abbreviated using the lexical syntax described in
Section 2.6. For example, "A string" abbreviates
[ 'A',' ','s','t','r', 'i','n','g']
Tuples are algebraic datatypes with special syntax, as defined in Section 3.8. Each tuple type has a single constructor. All tuples are instances of Eq, Ord, Bounded, Read, and Show (provided, of course, that all their component types are).
There is no upper bound on the size of a tuple, but some Haskell implementations may restrict the size of tuples, and limit the instances associated with larger tuples. However, every Haskell implementation must support tuples up to size 15, together with the instances for Eq, Ord, Bounded, Read, and Show. The Prelude and libraries define tuple functions such as zip for tuples up to a size of 7.
The constructor for a tuple is written by omitting the expressions surrounding the commas; thus (x,y) and (,) x y produce the same value. The same holds for tuple type constructors; thus, (Int,Bool,Int) and (,,) Int Bool Int denote the same type.
The following functions are defined for pairs (2-tuples): fst, snd, curry, and uncurry. Similar functions are not predefined for larger tuples.
IOError is an abstract type representing errors raised by I/O operations. It is an instance of Show and Eq. Values of this type are constructed by the various I/O functions and are not presented in any further detail in this report. The Prelude contains a few I/O functions (defined in Section A.3), and the Library Report contains many more.
| seq _|_b = _|_ |
| seq a b = b, if a /=_|_ |
seq is usually introduced to improve performance by avoiding unneeded laziness. Strict datatypes (see Section 4.2.1) are defined in terms of the $! operator. However, the provision of seq has important semantic consequences, because it is available at every type. As a consequence, _|_ is not the same as \x -> _|_, since seq can be used to distinguish them. For the same reason, the existence of seq weakens Haskell's parametricity properties.
The operator $! is strict (call-by-value) application, and is defined
in terms of seq. The Prelude also defines the $ operator to perform
non-strict application.
infixr 0 $, $!
($), ($!) :: (a -> b) -> a -> b
f $ x = f x
f $! x = x `seq` f x
The non-strict application operator $ may appear redundant, since
ordinary application (f x) means the same as (f $ x).
However, $ has low, right-associative binding precedence,
so it sometimes allows parentheses to be omitted; for example:
f $ g $ h x = f (g (h x))
It is also useful in higher-order situations, such as map ($ 0) xs,
or zipWith ($) fs xs.

Figure 5Standard Haskell Classes |
Default class method declarations (Section 4.3) are provided for many of the methods in standard classes. A comment with each class declaration in Appendix A specifies the smallest collection of method definitions that, together with the default declarations, provide a reasonable definition for all the class methods. If there is no such comment, then all class methods must be given to fully specify an instance.
This declaration gives default method declarations for both /= and ==, each being defined in terms of the other. If an instance declaration for Eq defines neither == nor /=, then both will loop. If one is defined, the default method for the other will make use of the one that is defined. If both are defined, neither default method is used.
The default declarations allow a user to create an Ord instance either with a type-specific compare function or with type-specific == and <= functions.
showsPrec and showList return a String-to-String function, to allow constant-time concatenation of its results using function composition. A specialised variant, show, is also provided, which uses precedence context zero, and returns an ordinary String. The method showList is provided to allow the programmer to give a specialised way of showing lists of values. This is particularly useful for the Char type, where values of type String should be shown in double quotes, rather than between square brackets.
Derived instances of Read and Show replicate the style in which a constructor is declared: infix constructors and field names are used on input and output. Strings produced by showsPrec are usually readable by readsPrec.
All Prelude types, except function types and IO types, are instances of Show and Read. (If desired, a programmer can easily make functions and IO types into (vacuous) instances of Show, by providing an instance declaration.)
For convenience, the Prelude provides the following auxiliary
functions:
reads :: (Read a) => ReadS a
reads = readsPrec 0
shows :: (Show a) => a -> ShowS
shows = showsPrec 0
read :: (Read a) => String -> a
read s = case [x | (x,t) <- reads s, ("","") <- lex t] of
[x] -> x
[] -> error "PreludeText.read: no parse"
_ -> error "PreludeText.read: ambiguous parse"
shows and reads use a default precedence of 0. The read function reads
input from a string, which must be completely consumed by the input
process.
The function lex :: ReadS String, used by read, is also part of the Prelude. It reads a single lexeme from the input, discarding initial white space, and returning the characters that constitute the lexeme. If the input string contains only white space, lex returns a single successful "lexeme" consisting of the empty string. (Thus lex "" = [("","")].) If there is no legal lexeme at the beginning of the input string, lex fails (i.e. returns []).
Instances of Enum may be derived for any enumeration type (types whose constructors have no fields); see Appendix C.
For any type that is an instance of class Bounded as well as Enum, the following should hold:
The following Prelude types are instances of Enum:
For the types Int and Integer, the enumeration functions have the following meaning:
For all four of these Prelude numeric types, all of the enumFrom family of functions are strict in all their arguments.
class Functor f where
fmap :: (a -> b) -> f a -> f b
The Functor
class is used for types that can be mapped over. Lists, IO, and
Maybe are in this class.
Instances of Functor should satisfy the following laws:
| fmap id | = | id |
| fmap (f . g) | = | fmap f . fmap g |
All instances of Functor defined in the Prelude satisfy these laws.
"do" expressions provide a convenient syntax for writing monadic expressions (see Section 3.14). The fail method is invoked on pattern-match failure in a do expression.
In the Prelude, lists, Maybe, and IO are all instances of Monad. The fail method for lists returns the empty list [], for Maybe returns Nothing, and for IO raises a user exception in the IO monad (see Section 7.3).
Instances of Monad should satisfy the following laws:
| return a >>= k | = | k a |
| m >>= return | = | m |
| m >>= (\x -> k x >>= h) | = | (m >>= k) >>= h |
Instances of both Monad and Functor should additionally satisfy the law:
| fmap f xs | = | xs >>= return . f |
All instances of Monad defined in the Prelude satisfy these laws.
The Prelude provides the following auxiliary functions:
sequence :: Monad m => [m a] -> m [a]
sequence_ :: Monad m => [m a] -> m ()
mapM :: Monad m => (a -> m b) -> [a] -> m [b]
mapM_ :: Monad m => (a -> m b) -> [a] -> m ()
(=<<) :: Monad m => (a -> m b) -> m a -> m b
The Bounded class is used to name the upper and lower limits of a type. Ord is not a superclass of Bounded since types that are not totally ordered may also have upper and lower bounds. The types Int, Char, Bool, (), Ordering, and all tuples are instances of Bounded. The Bounded class may be derived for any enumeration type; minBound is the first constructor listed in the data declaration and maxBound is the last. Bounded may also be derived for single-constructor datatypes whose constituent types are in Bounded.
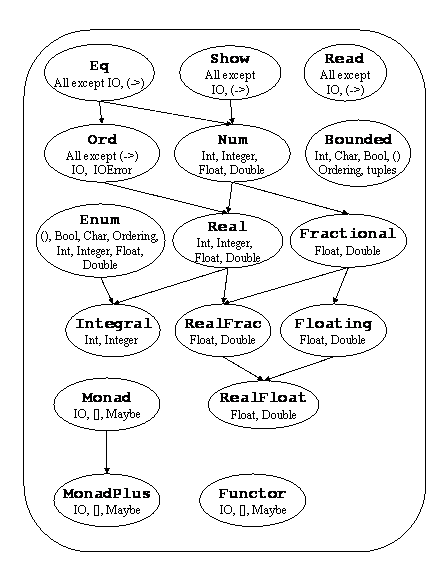
Haskell provides several kinds of numbers; the numeric types and the operations upon them have been heavily influenced by Common Lisp and Scheme. Numeric function names and operators are usually overloaded, using several type classes with an inclusion relation shown in Figure 5. The class Num of numeric types is a subclass of Eq, since all numbers may be compared for equality; its subclass Real is also a subclass of Ord, since the other comparison operations apply to all but complex numbers (defined in the Complex library). The class Integral contains integers of both limited and unlimited range; the class Fractional contains all non-integral types; and the class Floating contains all floating-point types, both real and complex.
The Prelude defines only the most basic numeric types: fixed sized integers (Int), arbitrary precision integers (Integer), single precision floating (Float), and double precision floating (Double). Other numeric types such as rationals and complex numbers are defined in libraries. In particular, the type Rational is a ratio of two Integer values, as defined in the Ratio library.
The default floating point operations defined by the Haskell Prelude do not conform to current language independent arithmetic (LIA) standards. These standards require considerably more complexity in the numeric structure and have thus been relegated to a library. Some, but not all, aspects of the IEEE floating point standard have been accounted for in Prelude class RealFloat.b
The standard numeric types are listed in Table 2. The finite-precision integer type Int covers at least the range [ - 229, 229 - 1]. As Int is an instance of the Bounded class, maxBound and minBound can be used to determine the exact Int range defined by an implementation. Float is implementation-defined; it is desirable that this type be at least equal in range and precision to the IEEE single-precision type. Similarly, Double should cover IEEE double-precision. The results of exceptional conditions (such as overflow or underflow) on the fixed-precision numeric types are undefined; an implementation may choose error (_|_, semantically), a truncated value, or a special value such as infinity, indefinite, etc.
| Type | Class | Description |
| Integer | Integral | Arbitrary-precision integers |
| Int | Integral | Fixed-precision integers |
| (Integral a) => Ratio a | RealFrac | Rational numbers |
| Float | RealFloat | Real floating-point, single precision |
| Double | RealFloat | Real floating-point, double precision |
| (RealFloat a) => Complex a | Floating | Complex floating-point |
The standard numeric classes and other numeric functions defined in the Prelude are shown in Figures 6--7. Figure 5 shows the class dependencies and built-in types that are instances of the numeric classes.
Figure 7Standard Numeric Classes and Related Operations, Part 2 |
The syntax of numeric literals is given in
Section 2.5. An integer literal represents the
application
of the function fromInteger to the appropriate
value of type
Integer. Similarly, a floating literal stands for an application of
fromRational to a value of type Rational (that is,
Ratio Integer). Given the typings:
fromInteger :: (Num a) => Integer -> a
fromRational :: (Fractional a) => Rational -> a
integer and floating literals have the
typings (Num a) => a and (Fractional a) => a, respectively.
Numeric literals are defined in this indirect way so that they may be
interpreted as values of any appropriate numeric type.
See Section 4.3.4 for a discussion of overloading ambiguity.
The infix class methods (+), (*), (-), and the unary function negate (which can also be written as a prefix minus sign; see section 3.4) apply to all numbers. The class methods quot, rem, div, and mod apply only to integral numbers, while the class method (/) applies only to fractional ones. The quot, rem, div, and mod class methods satisfy these laws if y is non-zero:
| (x `quot` y)*y + (x `rem` y) == x |
| (x `div` y)*y + (x `mod` y) == x |
`quot` is integer division truncated toward zero,
while the result of `div` is truncated toward
negative infinity.
The quotRem class method takes a dividend and a divisor as arguments
and returns a (quotient, remainder) pair; divMod is defined
similarly:
quotRem x y = (x `quot` y, x `rem` y)
divMod x y = (x `div` y, x `mod` y)
Also available on integral numbers are the even and odd predicates:
even x = x `rem` 2 == 0
odd = not . even
Finally, there are the greatest common divisor and least common
multiple functions. gcd x y is the greatest
(positive) integer that divides both x and y; for example gcd (-3) 6 = 3, gcd (-3) (-6) = 3,
gcd 0 4 = 4. gcd 0 0 raises a runtime error.
lcm x y is the smallest positive integer that both x and y divide.
The one-argument exponential function exp and the logarithm function log act on floating-point numbers and use base e. logBase a x returns the logarithm of x in base a. sqrt returns the principal square root of a floating-point number. There are three two-argument exponentiation operations: (^) raises any number to a nonnegative integer power, (^^) raises a fractional number to any integer power, and (**) takes two floating-point arguments. The value of x^0 or x^^0 is 1 for any x, including zero; 0**y is undefined.
A number has a magnitude
and a sign. The functions abs and
signum apply to any number and satisfy the law:
abs x * signum x == x
For real numbers, these functions are defined by:
abs x | x >= 0 = x
| x < 0 = -x
signum x | x > 0 = 1
| x == 0 = 0
| x < 0 = -1
Class Floating provides the circular and hyperbolic sine, cosine, and tangent functions and their inverses. Default implementations of tan, tanh, logBase, **, and sqrt are provided, but implementors are free to provide more accurate implementations.
Class RealFloat provides a version of arctangent taking two real floating-point arguments. For real floating x and y, atan2 y x computes the angle (from the positive x-axis) of the vector from the origin to the point (x,y). atan2 y x returns a value in the range [-pi, pi]. It follows the Common Lisp semantics for the origin when signed zeroes are supported. atan2 y 1, with y in a type that is RealFloat, should return the same value as atan y. A default definition of atan2 is provided, but implementors can provide a more accurate implementation.
The precise definition of the above functions is as in Common Lisp, which in turn follows Penfield's proposal for APL [9]. See these references for discussions of branch cuts, discontinuities, and implementation.
The ceiling, floor, truncate, and round functions each take a real fractional argument and return an integral result. ceiling x returns the least integer not less than x, and floor x, the greatest integer not greater than x. truncate x yields the integer nearest x between 0 and x, inclusive. round x returns the nearest integer to x, the even integer if x is equidistant between two integers.
The function properFraction takes a real fractional number x and returns a pair (n,f) such that x = n+f, and: n is an integral number with the same sign as x; and f is a fraction f with the same type and sign as x, and with absolute value less than 1. The ceiling, floor, truncate, and round functions can be defined in terms of properFraction.
Two functions convert numbers to type Rational: toRational returns the rational equivalent of its real argument with full precision; approxRational takes two real fractional arguments x and e and returns the simplest rational number within e of x, where a rational p/q in reduced form is simpler than another p' / q' if |p| <=|p'| and q <=q' . Every real interval contains a unique simplest rational; in particular, note that 0/1 is the simplest rational of all.
The class methods of class RealFloat allow efficient, machine-independent access to the components of a floating-point number. The functions floatRadix, floatDigits, and floatRange give the parameters of a floating-point type: the radix of the representation, the number of digits of this radix in the significand, and the lowest and highest values the exponent may assume, respectively. The function decodeFloat applied to a real floating-point number returns the significand expressed as an Integer and an appropriately scaled exponent (an Int). If decodeFloat x yields (m,n), then x is equal in value to mbn, where b is the floating-point radix, and furthermore, either m and n are both zero or else bd-1<=m<bd, where d is the value of floatDigits x. encodeFloat performs the inverse of this transformation. The functions significand and exponent together provide the same information as decodeFloat, but rather than an Integer, significand x yields a value of the same type as x, scaled to lie in the open interval (-1,1). exponent 0 is zero. scaleFloat multiplies a floating-point number by an integer power of the radix.
The functions isNaN, isInfinite, isDenormalized, isNegativeZero, and isIEEE all support numbers represented using the IEEE standard. For non-IEEE floating point numbers, these may all return false.
Also available are the following coercion functions:
fromIntegral :: (Integral a, Num b) => a -> b
realToFrac :: (Real a, Fractional b) => a -> b